Курс по LTspice, часть 4: Моделируем индуктивные компоненты
В силовой электронике индуктивные компоненты нередко становятся камнем преткновения, из-за которого девайс становится либо несуразно громоздким, либо наоборот вначале источает аромат перегревшейся изоляции, а затем раздается громкое БАХ взорвавшихся ключей. Поэтому нет никакого смысла приступать к макетированию будущего устройства без моделирования его параметров. Разработчик, пользующийся симулятором Swcad, должен достаточно ясно понимать те возможности и ограничения в части моделирования индуктивных компонентов, которые предоставляет ему этот симулятор.
Использование стандартного символа индуктивности “L” особых вопросов не вызывает. Наведя курсор на символ L и нажав на правую кнопку мыши, можно заполнить довольно большой список параметров модели, который содержит не только величину индуктивности, но также предельное значение амплитуды тока, значения эквивалентных последовательного и параллельного сопротивлений для учета омических потерь и величину паразитной параллельной емкости.Если эти детали не представляют интереса, можно ограничиться заданием значения индуктивности.
Индуктивный элемент также может быть представлен в виде генератора ЭДС самоиндукции с помощью символа функциональный источник напряжения “BV”, формульная строка которого строится по известному выражению U = L</di/dt. Оба этих варианта в виде простейших тестовых схем показаны на рис.1. Здесь же показаны прописи соответствующих строк редактора атрибутов BV. По сравнению со штатным второй вариант незначительно проигрывает ему в скорости счета, но в некоторых случаях его использование может оказаться полезным.
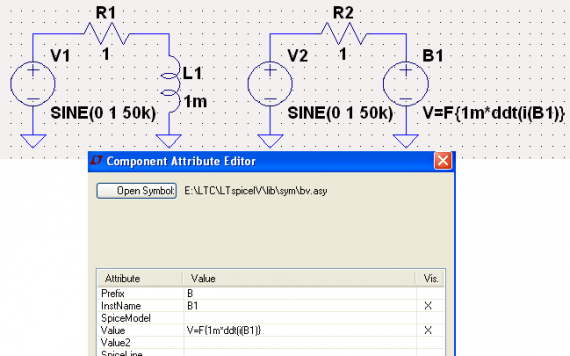
Рис.1
Нелинейные индуктивности, в качестве которых обычной практике используется ферромагнитный сердечник с обмоткой, в Swcad могут быть представлены двумя способами. В первом способе величина индуктивности изменяется в зависимости от величины протекающего через нее тока. Во втором способе используется гистерезисная модель Чана и др. Начнем с первого.
Этот способ основан на представлении процесса перемагничивания с помощью безгистерезисной кривой в виде гиперболического тангенса
B= tanh H
где B – индукция и H– напряженность магнитного поля.
Величина мгновенного значения H пропорциональна мгновенному значению протекающего тока i. Индуктивность L в свою очередь пропорциональна отношению B/H, которое в данном случае играет роль относительной проницаемости μ, модулирующей величину L.
В архиве моделей ltwiki.org/files/LTspiceIV.zip для Swcad можно найти тестовую схему модели нелинейной индуктивности, созданную по этому способу (LTspiceIV\examples\LTspiceWorldTour2009\Passives\Magnetics\Ind\ArbitareInductance).
В этой модели на вход нелинейной индуктивности подается линейно изменяющийся ток, имеющий di/dt=1. При таком возбуждении напряжение на индуктивности численно равно ее величине. Схема модели и результат запуска в режиме переходных процессов показаны на рис.2.
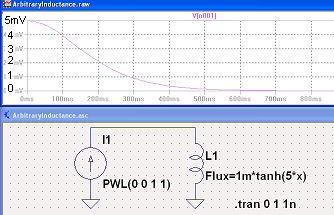
Рис.2
Из рис.2 нетрудно видеть, что при увеличении намагничивающего тока происходит снижение величины индуктивности от 5 мГн (напряжение 5 мВ) до весьма малых значений. Из этого следует, что при намагничивании переменным током в области максимальных значений тока напряжение на индуктивности будет минимальным, а области перехода через нуль – максимальным. Тестирование штатной модели нелинейной индуктивности при запитке от генератора тока подтверждает это соображение, а также показывает, что модель устойчиво работает в паре с генератором тока при любых разумных значениях возбуждающего тока.
Схема тестирования tanh-модели нелинейной индуктивности Swcad на частоте 50 кГц с запиткой от генератора тока показана на рис.3. Здесь же приведены результаты тестирования в виде графиков токов и напряжения на индуктивности для двух случаев:
— амплитуда тока достаточно мала (10 мА), чтобы не выходить за пределы относительно линейного участка,
— амплитуда тока (1 А) заведомо выводит индуктивность в область насыщения.
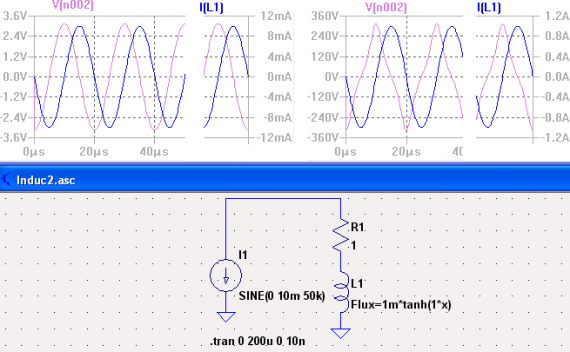
Рис.3
При запитке от генератора напряжения картина существенно меняется. Здесь уместно отметить, что режим запитки нелинейной индуктивности от генератора тока в практике не так уж часто встречается. Основной вид работы нелинейной индуктивности это параллельное подключение к генератору напряжения. Ярким тому примером является первичная обмотка силовых трансформаторов. Схема тестирования модели приведена на рис.4.
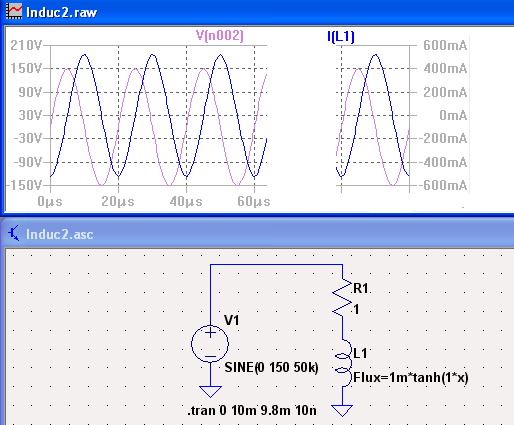
Рис.4
Тестирование модели нелинейной безгистерезисной индуктивности, созданной по первому способу, при возбуждении от генератора напряжения, показывает, что эта модель работоспособна в ограниченном интервале входных напряжений, в котором величина аргумента функции tanh не превышает 0.6 – 0.7. Это соответствует практически линейной модели с очень слабо выраженным эффектом насыщения. При увеличении аргумента tanh выше указанных значений возникают неразрешимые проблемы со сходимостью. Можно предположить, что причиной этого являются некие особенности программной реализации модели, которые не позволяют ей отрабатывать произвольное значение свободной составляющей тока переходного процесса при скачкообразном включении синусоидального напряжения. В результате модель нелинейной индуктивности с использованием проебразующей функции tanh имеет ограниченную область применения, а в ряде случаев может оказаться непригодной.
Обратимся ко второму способу создания модели нелинейной индуктивности, а именно к использованию модели Чана. Эта модель выгодно отличается от других известных моделей намагничивания ферромагнитных сердечников тем, что в ней во-первых непосредственно используются справочные параметры материала сердечника, публикуемые производителями, и конструктивные параметры узла (площадь сечения магнитопровода A, длина пути магнитной линии Lm, число витков N и величина воздушного зазора Lg), а во-вторых математическая подоснова модели содержит только простейшие арифметические операции.
Модель Чана основана на представлении магнитных свойств материала в виде петли гистерезиса предельного цикла намагничивания, который образуется тремя кривыми:
— верхняя ветвь гистерезисного цикла, вычисляемая по формуле
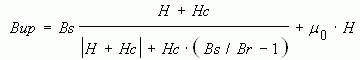
— нижняя ветвь, вычисляемая по формуле
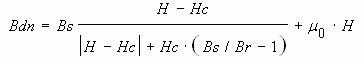
— полусумма верхней и нижней ветвей используется как кривая начального намагничивания.
Здесь
Bs – индукция насыщения, которая определяется в состоянии технического насыщения сердечника при напряженности поля 800…1000 А/м;
H – напряженность поля в А/м, для сердечника без зазора H = i·N/Lm;
Hc – коэрцитивная сила;
Br – остаточная индукция в предельном цикле.
Вид кривой гистерезисного цикла показан на рис.5
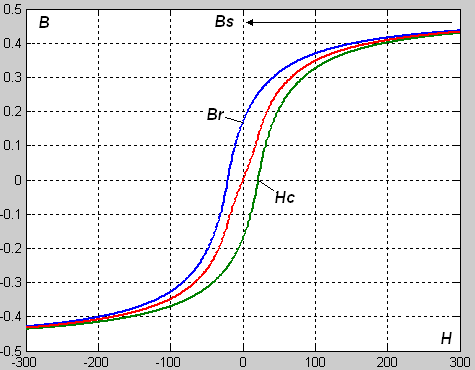
Рис.5
Пример тестирования модели Чана на популярном сердечнике Е65 из материала N87 фирмы Epcos при запитке от генератора напряжения приведен на рис.6. Параметры сердечника:
Bs = 0.49, Hc = 21, Bs =0.175, A = 0.00053 м2, Lm =0.147 м, Lg = 0, N = 10. На рис.6 приведены результаты тестирования в двух режимах: при номинальном подводимом напряжении и при сильной перегрузке повышенным напряжением.
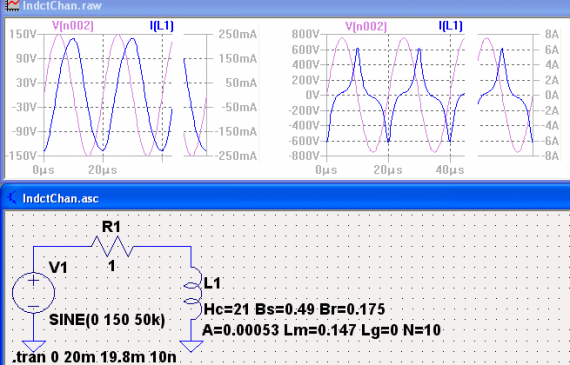
Рис.6
Как показывают осциллограммы токов, при номинальном напряжении искажения синусоиды невелики и в основном обусловлены проявлением гистерезиса. При увеличении напряжения в 5 раз наблюдаются сильные искажения формы ранее синусоидального тока из-за насыщения сердечника. При этом амплитуда тока увеличивается более чем 25 раз.
Результаты тестирования модели Чана при запитке нелинейной индуктивности от генератора тока показаны на рис.7. Естественно, что в этом случае искажения должны сказываться на форме напряжения. При возбуждении током близким к номинальному напряжение на индуктивности по форме напоминает синусоиду, но достаточно заметны искажения гистерезисного происхождения. При увеличении тока в 7 раз искажения заметно увеличиваются из-за входа сердечника в насыщение. При этом амплитуда пиков напряжения растет непропорционально быстрее.
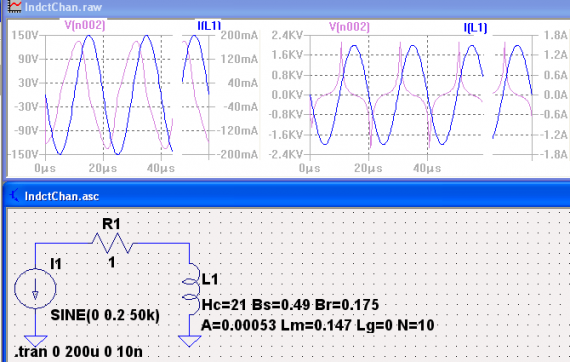
Рис.7
Таким образом, из двух способов построения модели нелинейной индуктивности в симуляторе Swcad универсальным может служить построение на основе модели Чана. Модель с нелинейным преобразованием с помощью функции tanh может иметь ограниченное применение преимущественно в схемах, где источник сигнала по своим выходным характеристикам близок к генератору тока. Общим недостатком обоих вариантов моделей является отсутствие возможности учета частотнозависимых потерь. Кроме того, оба варианта неприменимы для моделирования трансформаторной связи на основе представлений о взаимоиндуктивности.
Отметим также, что описанное выше использование модели Чана относится только к магнитопроводам простейшей формы, которые можно свести к одиночному замкнутому контуру с неизменной площадью сечения. Однако в устройствах автоматики и телемеханики находят применение и более сложные магнитопроводы с несколькими параллельными ветвями, имеющими независимые обмотки. В силовых преобразователях высокого уровня мощности встречается так называемое «магнитное ухо». Симулирование работы подобных устройств с помощью модели Чана в принципе возможно, но представляет отдельную задачу, требующую самостоятельного рассмотрения.
Использование стандартного символа индуктивности “L” особых вопросов не вызывает. Наведя курсор на символ L и нажав на правую кнопку мыши, можно заполнить довольно большой список параметров модели, который содержит не только величину индуктивности, но также предельное значение амплитуды тока, значения эквивалентных последовательного и параллельного сопротивлений для учета омических потерь и величину паразитной параллельной емкости.Если эти детали не представляют интереса, можно ограничиться заданием значения индуктивности.
Индуктивный элемент также может быть представлен в виде генератора ЭДС самоиндукции с помощью символа функциональный источник напряжения “BV”, формульная строка которого строится по известному выражению U = L</di/dt. Оба этих варианта в виде простейших тестовых схем показаны на рис.1. Здесь же показаны прописи соответствующих строк редактора атрибутов BV. По сравнению со штатным второй вариант незначительно проигрывает ему в скорости счета, но в некоторых случаях его использование может оказаться полезным.

Рис.1
Нелинейные индуктивности, в качестве которых обычной практике используется ферромагнитный сердечник с обмоткой, в Swcad могут быть представлены двумя способами. В первом способе величина индуктивности изменяется в зависимости от величины протекающего через нее тока. Во втором способе используется гистерезисная модель Чана и др. Начнем с первого.
Этот способ основан на представлении процесса перемагничивания с помощью безгистерезисной кривой в виде гиперболического тангенса
B= tanh H
где B – индукция и H– напряженность магнитного поля.
Величина мгновенного значения H пропорциональна мгновенному значению протекающего тока i. Индуктивность L в свою очередь пропорциональна отношению B/H, которое в данном случае играет роль относительной проницаемости μ, модулирующей величину L.
В архиве моделей ltwiki.org/files/LTspiceIV.zip для Swcad можно найти тестовую схему модели нелинейной индуктивности, созданную по этому способу (LTspiceIV\examples\LTspiceWorldTour2009\Passives\Magnetics\Ind\ArbitareInductance).
В этой модели на вход нелинейной индуктивности подается линейно изменяющийся ток, имеющий di/dt=1. При таком возбуждении напряжение на индуктивности численно равно ее величине. Схема модели и результат запуска в режиме переходных процессов показаны на рис.2.

Рис.2
Из рис.2 нетрудно видеть, что при увеличении намагничивающего тока происходит снижение величины индуктивности от 5 мГн (напряжение 5 мВ) до весьма малых значений. Из этого следует, что при намагничивании переменным током в области максимальных значений тока напряжение на индуктивности будет минимальным, а области перехода через нуль – максимальным. Тестирование штатной модели нелинейной индуктивности при запитке от генератора тока подтверждает это соображение, а также показывает, что модель устойчиво работает в паре с генератором тока при любых разумных значениях возбуждающего тока.
Схема тестирования tanh-модели нелинейной индуктивности Swcad на частоте 50 кГц с запиткой от генератора тока показана на рис.3. Здесь же приведены результаты тестирования в виде графиков токов и напряжения на индуктивности для двух случаев:
— амплитуда тока достаточно мала (10 мА), чтобы не выходить за пределы относительно линейного участка,
— амплитуда тока (1 А) заведомо выводит индуктивность в область насыщения.

Рис.3
При запитке от генератора напряжения картина существенно меняется. Здесь уместно отметить, что режим запитки нелинейной индуктивности от генератора тока в практике не так уж часто встречается. Основной вид работы нелинейной индуктивности это параллельное подключение к генератору напряжения. Ярким тому примером является первичная обмотка силовых трансформаторов. Схема тестирования модели приведена на рис.4.

Рис.4
Тестирование модели нелинейной безгистерезисной индуктивности, созданной по первому способу, при возбуждении от генератора напряжения, показывает, что эта модель работоспособна в ограниченном интервале входных напряжений, в котором величина аргумента функции tanh не превышает 0.6 – 0.7. Это соответствует практически линейной модели с очень слабо выраженным эффектом насыщения. При увеличении аргумента tanh выше указанных значений возникают неразрешимые проблемы со сходимостью. Можно предположить, что причиной этого являются некие особенности программной реализации модели, которые не позволяют ей отрабатывать произвольное значение свободной составляющей тока переходного процесса при скачкообразном включении синусоидального напряжения. В результате модель нелинейной индуктивности с использованием проебразующей функции tanh имеет ограниченную область применения, а в ряде случаев может оказаться непригодной.
Обратимся ко второму способу создания модели нелинейной индуктивности, а именно к использованию модели Чана. Эта модель выгодно отличается от других известных моделей намагничивания ферромагнитных сердечников тем, что в ней во-первых непосредственно используются справочные параметры материала сердечника, публикуемые производителями, и конструктивные параметры узла (площадь сечения магнитопровода A, длина пути магнитной линии Lm, число витков N и величина воздушного зазора Lg), а во-вторых математическая подоснова модели содержит только простейшие арифметические операции.
Модель Чана основана на представлении магнитных свойств материала в виде петли гистерезиса предельного цикла намагничивания, который образуется тремя кривыми:
— верхняя ветвь гистерезисного цикла, вычисляемая по формуле
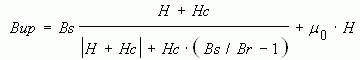
— нижняя ветвь, вычисляемая по формуле
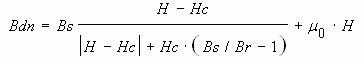
— полусумма верхней и нижней ветвей используется как кривая начального намагничивания.
Здесь
Bs – индукция насыщения, которая определяется в состоянии технического насыщения сердечника при напряженности поля 800…1000 А/м;
H – напряженность поля в А/м, для сердечника без зазора H = i·N/Lm;
Hc – коэрцитивная сила;
Br – остаточная индукция в предельном цикле.
Вид кривой гистерезисного цикла показан на рис.5

Рис.5
Пример тестирования модели Чана на популярном сердечнике Е65 из материала N87 фирмы Epcos при запитке от генератора напряжения приведен на рис.6. Параметры сердечника:
Bs = 0.49, Hc = 21, Bs =0.175, A = 0.00053 м2, Lm =0.147 м, Lg = 0, N = 10. На рис.6 приведены результаты тестирования в двух режимах: при номинальном подводимом напряжении и при сильной перегрузке повышенным напряжением.

Рис.6
Как показывают осциллограммы токов, при номинальном напряжении искажения синусоиды невелики и в основном обусловлены проявлением гистерезиса. При увеличении напряжения в 5 раз наблюдаются сильные искажения формы ранее синусоидального тока из-за насыщения сердечника. При этом амплитуда тока увеличивается более чем 25 раз.
Результаты тестирования модели Чана при запитке нелинейной индуктивности от генератора тока показаны на рис.7. Естественно, что в этом случае искажения должны сказываться на форме напряжения. При возбуждении током близким к номинальному напряжение на индуктивности по форме напоминает синусоиду, но достаточно заметны искажения гистерезисного происхождения. При увеличении тока в 7 раз искажения заметно увеличиваются из-за входа сердечника в насыщение. При этом амплитуда пиков напряжения растет непропорционально быстрее.

Рис.7
Таким образом, из двух способов построения модели нелинейной индуктивности в симуляторе Swcad универсальным может служить построение на основе модели Чана. Модель с нелинейным преобразованием с помощью функции tanh может иметь ограниченное применение преимущественно в схемах, где источник сигнала по своим выходным характеристикам близок к генератору тока. Общим недостатком обоих вариантов моделей является отсутствие возможности учета частотнозависимых потерь. Кроме того, оба варианта неприменимы для моделирования трансформаторной связи на основе представлений о взаимоиндуктивности.
Отметим также, что описанное выше использование модели Чана относится только к магнитопроводам простейшей формы, которые можно свести к одиночному замкнутому контуру с неизменной площадью сечения. Однако в устройствах автоматики и телемеханики находят применение и более сложные магнитопроводы с несколькими параллельными ветвями, имеющими независимые обмотки. В силовых преобразователях высокого уровня мощности встречается так называемое «магнитное ухо». Симулирование работы подобных устройств с помощью модели Чана в принципе возможно, но представляет отдельную задачу, требующую самостоятельного рассмотрения.

2 комментария
Что же касается коэффициента связи, то его величина зависит от конструкции индуктивного элемента. К примеру в трансформаторах на Ш-сердечниках с расположением обмотки на среднем керне это не менее 0,99. На кольцевых сердечниках с равномерным распределением обмоток по периметру не менее 0,995. Если обмотки разнесены по магнитопроводу, то коэффициент связи может заметно понижаться.