Цифровой задатчик интенсивности
При разработке механизмов движения, иногда, требуется обеспечить постоянство характеристик разгона и торможения. Другим словом необходимо обеспечить постоянные ускорения.
Предположим, что у нас имеется электропривод, у которого скорость и ускорение задаются в процентах: от 0 до 100% скорости и от 0 до 100% достижения этой скорости в секунду. Немного теории и никакой практики под катом.

Для Таких вещей требуется задатчик интенсивности. Функционально, задатчик интенсивности состоит из сумматора, трехпозиционного релейного элемента и интегратора.
Задача трехпозиционного релейного блока заключается в том, что если система создает ошибку, большую порогового значения, на выходе релейного блока будет константа со знаком ошибки. Задавая необходимую величину константы мы обеспечим нужную нам скорость нарастания выходного сигнала.
Задача интегратора — интегрировать.
Опишем все это дело. Итак, на входе у нас скорость задания Uз, а на выходе скорость на привод Uз`. После сумматора возникает ошибка e=U-Uз`` которую мы и подаем на релейный элемент. Передаточная функция релейного блока будет выглядеть следующим образом:

где k = наша минимальная величина погрешности.
Передаточная функция интегратора выглядит гораздо проще:

красиво выглядит, не правда ли? Но все так красиво только в комплексной плоскости. А поскольку у нас микропроцессорная система, преобразуем наши блоки из непрерывных в дискретные.
Для релейного блока все выглядит очень просто:
А с интегратором придется взяться за листок бумаги и ручку.
Преобразуем функцию (2) в следующий вид:
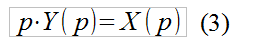
и преобразуем комплексные величины по следующей формуле:
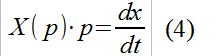
Получим передаточную функцию интегратора в реальном времени:

Учтем дискретность:

гдеYk, Yk-1 — это текущее и предыдущее выходные значения, Xk — текущее входное значение, Ts — период квантования. Выразим отсюда Yk:

Готово! Полученное разностное уравнение мы можем реализовать в программном коде. По предыдущему куску кода может быть кто-то уже догадался, что делать мы это будем в пакете моделирования Scilab. Кому надо, тот вполне реализует этот код и на микроконтроллере
Период дискретности у меня 10мс. Как я сказал ранее, задачей у меня было обеспечить изменение скорости от 0 до 100% от максимальной за 1 секунду, если ускорение выставлено 100%. Соответственно, при ускорении в 50% выход на максимальную скорость будет 2с, 25% 4 секунды и т. д.
Проверяем:

По оси Y у нас значение скорости, по Оси X количество отсчетов. в 1с — 100 отсчетов.
На данном графике представлено моделирование разгона от 0 до 100% скорости при ускорении в 25%, 50%, 100% (графики справа-на-лево). Как видно, время разгона составляет соответственно 4с, 2с, 1с, что соответствует условию.
Разумеется, Это у меня числа такие красивые. В реальных условиях скорее всего придется ускорения в абсолютных числах. Тут уже потребуется методично рассчитывать коэффициент интегратора, но это уже совсем другая история.
Для изучения ТАУ рекомендую книгу Бессекерский. Теория Автоматического Управления.
Предположим, что у нас имеется электропривод, у которого скорость и ускорение задаются в процентах: от 0 до 100% скорости и от 0 до 100% достижения этой скорости в секунду. Немного теории и никакой практики под катом.

Для Таких вещей требуется задатчик интенсивности. Функционально, задатчик интенсивности состоит из сумматора, трехпозиционного релейного элемента и интегратора.
Задача трехпозиционного релейного блока заключается в том, что если система создает ошибку, большую порогового значения, на выходе релейного блока будет константа со знаком ошибки. Задавая необходимую величину константы мы обеспечим нужную нам скорость нарастания выходного сигнала.
Задача интегратора — интегрировать.
Опишем все это дело. Итак, на входе у нас скорость задания Uз, а на выходе скорость на привод Uз`. После сумматора возникает ошибка e=U-Uз`` которую мы и подаем на релейный элемент. Передаточная функция релейного блока будет выглядеть следующим образом:

где k = наша минимальная величина погрешности.
Передаточная функция интегратора выглядит гораздо проще:

красиво выглядит, не правда ли? Но все так красиво только в комплексной плоскости. А поскольку у нас микропроцессорная система, преобразуем наши блоки из непрерывных в дискретные.
Для релейного блока все выглядит очень просто:
if (abs(SpeedError)>SetPointError) then
RelayOut=Boost;
else RelayOut=0;
end
А с интегратором придется взяться за листок бумаги и ручку.
Преобразуем функцию (2) в следующий вид:
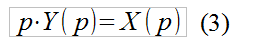
и преобразуем комплексные величины по следующей формуле:
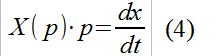
Получим передаточную функцию интегратора в реальном времени:

Учтем дискретность:

гдеYk, Yk-1 — это текущее и предыдущее выходные значения, Xk — текущее входное значение, Ts — период квантования. Выразим отсюда Yk:

Готово! Полученное разностное уравнение мы можем реализовать в программном коде. По предыдущему куску кода может быть кто-то уже догадался, что делать мы это будем в пакете моделирования Scilab. Кому надо, тот вполне реализует этот код и на микроконтроллере
SetPointError=0.1;//погрешность установки скорости
Boost=25;//ускорение
Speed=100;//задаваемая скорость
SpeedDash=0;//выходное значение скорости
SpeedDashOld=0;//старое значение
Ts=0.01;//период дискретности
i=1;
//цикл нужен только в моделировании. в реальном устройстве это бесконечные вычисленияю
while(abs(Speed)>abs(SpeedDash))//пока не достигли скорости
SpeedError=Speed-SpeedDash;//ошибка скорости
if (abs(SpeedError)>SetPointError) then//пока ошибка больше допустимой
RelayOut=Boost;//выход релейного элемента
else RelayOut=0;
end
SpeedDash=RelayOut*(Ts)+SpeedDashOld;//интегрируем скорость
OutValue(i)=SpeedDash;//создаем массив для графика
i=i+1;
SpeedDashOld=SpeedDash;//запоминаем предыдуее значение
end
t=1:i-1;
figure(0);
plot2d(t,OutValue);//рисуем красивый графикПериод дискретности у меня 10мс. Как я сказал ранее, задачей у меня было обеспечить изменение скорости от 0 до 100% от максимальной за 1 секунду, если ускорение выставлено 100%. Соответственно, при ускорении в 50% выход на максимальную скорость будет 2с, 25% 4 секунды и т. д.
Проверяем:

По оси Y у нас значение скорости, по Оси X количество отсчетов. в 1с — 100 отсчетов.
На данном графике представлено моделирование разгона от 0 до 100% скорости при ускорении в 25%, 50%, 100% (графики справа-на-лево). Как видно, время разгона составляет соответственно 4с, 2с, 1с, что соответствует условию.
Разумеется, Это у меня числа такие красивые. В реальных условиях скорее всего придется ускорения в абсолютных числах. Тут уже потребуется методично рассчитывать коэффициент интегратора, но это уже совсем другая история.
Для изучения ТАУ рекомендую книгу Бессекерский. Теория Автоматического Управления.

3 комментария
Один из простых методов преобразования одной переменной в другое — метод линеаризации. Про него будет моя сегодняшняя статья.